Before I begin, there is one thing you need to understand: every event has a time and a place. An event happening in Sacramento and New York at the same exact time is not the same event because they’re happening in different places. An event in Sacramento in June is not the same event as one that’s happening in Sacramento in August because they’re at different times. But, if an event happens at the same time and at the same place, then it’s the same event. Got it?
Some things you should know about Figure 1 below [1]:
- In Figure 1, there's a rectangular box. At the bottom of the box is a light source.
- On the other side of the box is a mirror reflecting that light source.
- There are two events happening in the image. Event A is when the light leaves the light source. Event B is when the light returns to the light source after hitting the mirror.
- The box is on a conveyor belt moving to the right at a constant speed.
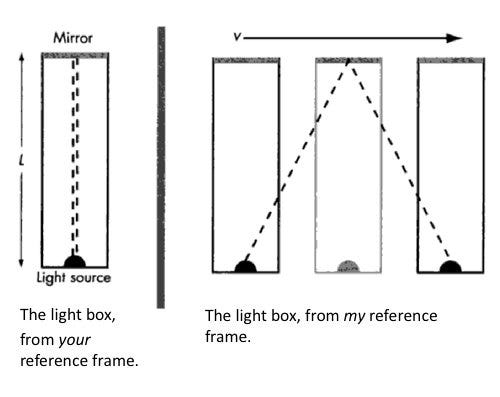
As a punishment, you got put inside the box and are stuck in it. What you see is on the left side of the image. Since you're moving with the box, Events A and B occur at the same place: Point W.
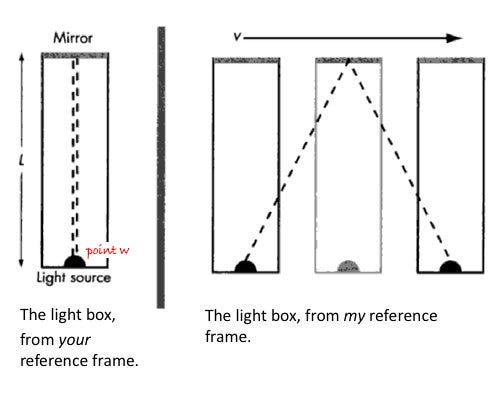
We know the speed of light, c, travels at 186,000 miles per second and we also know that speed c is constant and cannot move any faster or slower (this is part of the general Principle of Relativity).
Inside the box, you measure the time between event A and event B as taking 0:00:01 seconds.
The right side of the image shows what I see as I look at the box from above the conveyor belt. I’m in charge of making sure you don’t jump out and escape your punishment.
Since the box is moving to the right of me, I observe events A and B occurring at different locations. Event A happens at point X and event B happens at point Y.
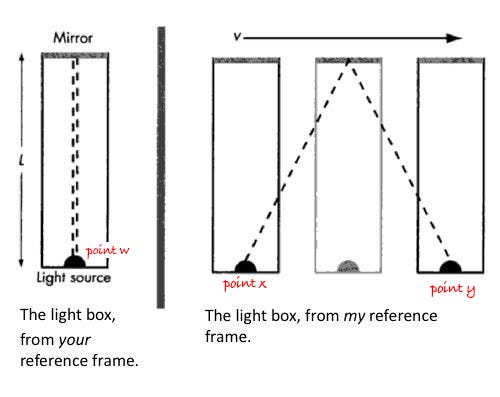
Since I see the light as now traveling in a diagonal and therefore having to go a further distance than it would if it were moving in a straight line, I can conclude it took longer for event B to occur after event A than it did for you. In this case, the time between event A and event B was measured at 0:00:01.07.
Therefore, you experienced time moving slower by .07 seconds than I did.
To clarify: these aren’t two different events. It’s the same event happening at the same time and the same place but viewed from two different reference frames. In the reference frame inside the box, events A and B happen in the same location. In a reference frame outside of the box, events A and B happen at different locations, namely X and Y.
So you, the person inside the box, are seeing the events occur at the same place and saying 0:00:01 seconds elapsed between the two.
I'm saying 0:00:01.07 seconds elapsed between the two.
This is time dilation.
The formal (yet simple) definition of time dilation is:
The time between two events is shortest when measured in a reference frame from where the two events occur at the same place.
For you, the person in the box that was moving on the conveyor belt relative to me, the light took 0:00:01 seconds to get from event A to event B. That's correct. That's how long it took.
But for me, the person that's not moving relative to the box, I saw the light take a longer path. Therefore, it had to take a longer amount of time than for you, which is why I measured 0:00:01.07 seconds between events A and B.
Therefore, we can conclude that time moved slower for you, and in this example, 0:00:00.07 seconds slower than time moved for me.
Note: The time allotted here is purely for example purposes and not real. I’m using the two times to demonstrate time dilation and not using the actual formula. Using the actual formula, an event that a stationary observer says took 0.1 seconds, an observer moving at 124,274.2 miles/second would see it take 0.1342385 seconds.
How to time travel
We can use time dilation to time travel.
To illustrate this, let’s look at two co-workers: Stella and Earl.
Stella wants to see what a star looks like in space, so she boards a spaceship and travels 186,000 miles per second and zooms off to a star in our galaxy, and comes back.
To Stella, the trip only takes a few days. But when she comes back, Earl is 20 years older!
Stella time-traveled 20 years into the future.
How did this happen? Time dilation.
Since the two events happened in the same place for Stella (event A is when she left Earth and event B is when she returned) and she was moving at near the speed of light, she experienced time moving more slowly than Earl did, which is why the trip took only a few days. For Earl, the trip took 20 years!
This thought experiment was demonstrated by a test conducted in the 70s with atomic clocks.
Named the Hafele–Keating experiment, after scientists Joseph C. Hafele and Richard E. Keating, researchers sent atomic clocks around the world aboard commercial airliners. When they returned, they compared their results to atomic clocks that stayed resting on the ground.
Here are the results:
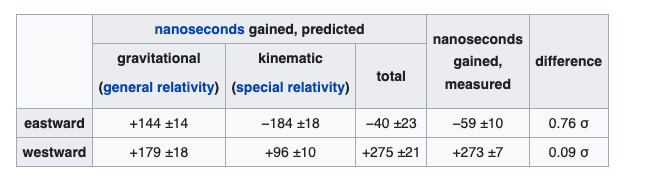
As an example (it wasn’t really this dramatic), the clock on the ground elapsed 10 hours between takeoff and landing while the clock on the plane only elapsed 9 hours between the same takeoff and the same landing. In reality, the clocks gained about 0.15 microseconds compared to the stationary clock [2].
The clock would then be 1 hour "into the future."
This is how Stella did time traveled.
The clocks (and Stella) experienced a change in gravity as they got further from the center of Earth’s gravitational pull. As gravity decreases the further something gets in the atmosphere, the faster time will move.
Counter-acting that effect is special relativity’s time dilation caused by velocity, which is what we experienced with the boxes. The faster one’s relative velocity is compared to a stationary observer, the slower it will experience time in a reference frame from the observer.
Therefore, if you had a spaceship that could travel near the speed of light, you could time travel because you’d be moving so fast that time essentially comes to a halt [3]. Hopefully, you like what you discover, because you couldn’t ever come back.
Note: Time dilation effects aren’t noticeable unless you’re traveling at or near the speed of light. This is why it’s not something you have to deal with on a day-to-day basis and also why the effects were so minimal in the Hafele–Keating experiment.
Note 2: I am no physicist. I’m a curious person who reads books and tries to understand things and in the process, teach myself and try to teach others. I may have gotten some details wrong, but I tried to be certain of what I published. As I understand time dilation, and it’s a simple understanding I have, this is how it would work. If I’m wrong about something, please correct me and point me somewhere I can learn about my mistakes.
Tagged